Kepler's laws of planetary motion

1. For a more historical approach, see in particular the articles Astronomia nova and Epitome Astronomiae Copernicanae.
   In astronomy, Kepler's laws of planetary motion are three scientific laws describing the motion of planets around the Sun.
   
   
   Figure 1: Illustration of Kepler's three laws with two planetary orbits.
   (1) The orbits are ellipses, with focal points ƒ₁ and ƒ₂ for the first planet and ƒ₁ and ƒ₃ for the second planet. The Sun is placed in focal point ƒ₁.
   
   (2) The two shaded sectors A₁ and A₂ have the same surface area and the time for planet 1 to cover segment A₁ is equal to the time to cover segment A₂.
   
   (3) The total orbit times for planet 1 and planet 2 have a ratio a₁^3/2 : a₂^3/2.

   Astrodynamics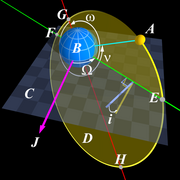
   Orbital mechanics
   Equations[hide] Kepler's laws Tsiolkovsky rocket equation Vis-viva equation
   Efficiency measures[show]
   v t e

   1. The orbit of a planet is an ellipse with the Sun at one of the two foci.
   2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.^[1]
   3. The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
   Most planetary orbits are nearly circular, and careful observation and calculation are required in order to establish that they are not perfectly circular. Calculations of the orbit of Mars, whose published values are somewhat suspect,^[2] indicated an elliptical orbit. From this, Johannes Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits.
   Kepler's work (published between 1609 and 1619) improved the heliocentric theory of Nicolaus Copernicus, explaining how the planets' speeds varied, and using elliptical orbits rather than circular orbits with epicycles.^[3]
   Isaac Newton showed in 1687 that relationships like Kepler's would apply in the Solar System to a good approximation, as a consequence of his own laws of motion and law of universal gravitation.
   Kepler's laws are part of the foundation of modern astronomy and physics.^[4]
   

   Contents

   • 1 Comparison to Copernicus
   • 2 Nomenclature
   • 3 History
   • 4 Formulary
     • 4.1 First law
     • 4.2 Second law
     • 4.3 Third law
   • 5 Planetary acceleration
     • 5.1 Acceleration vector
     • 5.2 The inverse square law
     • 5.3 Newton's law of gravitation
   • 6 Position as a function of time
     • 6.1 Mean anomaly, M
     • 6.2 Eccentric anomaly, E
     • 6.3 True anomaly, θ
     • 6.4 Distance, r
   • 7 See also
   • 8 Notes
   • 9 References
   • 10 Bibliography
   • 11 External links

   Comparison to Copernicus

   Kepler's laws improve the model of Copernicus. If the eccentricities of the planetary orbits are taken as zero, then Kepler basically agrees with Copernicus:
   
   1. The planetary orbit is a circle
   2. The Sun is at the center of the orbit
   3. The speed of the planet in the orbit is constant
   The eccentricities of the orbits of those planets known to Copernicus and Kepler are small, so the foregoing rules give good approximations of planetary motion; but Kepler's laws fit the observations better than Copernicus'.
   Kepler's corrections are not at all obvious:
   
   1. The planetary orbit is not a circle, but an ellipse.
   2. The Sun is not at the center but at a focal point of the elliptical orbit.
   3. Neither the linear speed nor the angular speed of the planet in the orbit is constant, but the area speed is constant.
   The eccentricity of the orbit of the Earth makes the time from the March equinox to the September equinox, around 186 days, unequal to the time from the September equinox to the March equinox, around 179 days. A diameter would cut the orbit into equal parts, but the plane through the Sun parallel to the equator of the Earth cuts the orbit into two parts with areas in a 186 to 179 ratio, so the eccentricity of the orbit of the Earth is approximately
   

   ${\displaystyle \varepsilon \approx {\frac {\pi }{4}}{\frac {186-179}{186+179}}\approx 0.015,}$

   which is close to the correct value (0.016710219) (see Earth's orbit). The calculation is correct when perihelion, the date the Earth is closest to the Sun, falls on a solstice. The current perihelion, near January 4, is fairly close to the solstice of December 21 or 22.
   

   Nomenclature

   It took nearly two centuries for the current formulation of Kepler's work to take on its settled form. Voltaire's Eléments de la philosophie de Newton (Elements of Newton's Philosophy) of 1738 was the first publication to use the terminology of "laws".^[5][6] The Biographical Encyclopedia of Astronomers in its article on Kepler (p. 620) states that the terminology of scientific laws for these discoveries was current at least from the time of Joseph de Lalande.^[7] It was the exposition of Robert Small, in An account of the astronomical discoveries of Kepler (1804) that made up the set of three laws, by adding in the third.^[8] Small also claimed, against the history, that these were empirical laws, based on inductive reasoning.^[6][9]
   Further, the current usage of "Kepler's Second Law" is something of a misnomer. Kepler had two versions, related in a qualitative sense: the "distance law" and the "area law." The "area law" is what became the Second Law in the set of three; but Kepler did himself not privilege it in that way.^[10]
   

   History

   Johannes Kepler published his first two laws about planetary motion in 1609, having found them by analyzing the astronomical observations of Tycho Brahe.^[11][3][12] Kepler's third law was published in 1619.^[13][3] Notably, Kepler had believed in the Copernican model of the solar system, which called for circular orbits, but could not reconcile Brahe's highly precise observations with a circular fit to Mars' orbit (Mars coincidentally having the highest eccentricity of all planets except Mercury^[14]). His first law reflected this discovery.
   Kepler in 1621 and Godefroy Wendelin in 1643 noted that Kepler's third law applies to the four brightest moons of Jupiter.^{[Nb 1]} The second law, in the "area law" form, was contested by Nicolaus Mercator in a book from 1664, but by 1670 his Philosophical Transactions were in its favour. As the century proceeded it became more widely accepted.^[15] The reception in Germany changed noticeably between 1688, the year in which Newton's Principia was published and was taken to be basically Copernican, and 1690, by which time work of Gottfried Leibniz on Kepler had been published.^[16]
   Newton is credited with understanding that the second law is not special to the inverse square law of gravitation, being a consequence just of the radial nature of that law; while the other laws do depend on the inverse square form of the attraction. Carl Runge and Wilhelm Lenz much later identified a symmetry principle in the phase space of planetary motion (the orthogonal group O(4) acting) which accounts for the first and third laws in the case of Newtonian gravitation, as conservation of angular momentum does via rotational symmetry for the second law.^[17]
   

   Formulary

   The mathematical model of the kinematics of a planet subject to the laws allows a large range of further calculations.
   

   First law

   The orbit of every planet is an ellipse with the Sun at one of the two foci.
   

   
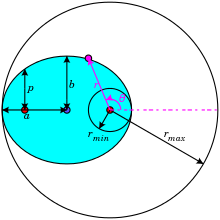
   Figure 2: Kepler's first law placing the Sun at the focus of an elliptical orbit
   
   Figure 4: Heliocentric coordinate system (r, θ) for ellipse. Also shown are: semi-major axis a, semi-minor axis b and semi-latus rectum p; center of ellipse and its two foci marked by large dots. For θ = 0°, r = r_min and for θ = 180°, r = r_max.
   Mathematically, an ellipse can be represented by the formula:
   

   ${\displaystyle r={\frac {p}{1+\varepsilon \,\cos \theta }},}$

   where ${\displaystyle p}$ is the semi-latus rectum, ε is the eccentricity of the ellipse, r is the distance from the Sun to the planet, and θ is the angle to the planet's current position from its closest approach, as seen from the Sun. So (r, θ) are polar coordinates.
   For an ellipse 0 < ε < 1 ; in the limiting case ε = 0, the orbit is a circle with the sun at the centre (i.e. where there is zero eccentricity).
   At θ = 0°, perihelion, the distance is minimum
   

   ${\displaystyle r_{\min }={\frac {p}{1+\varepsilon }}}$

   At θ = 90° and at θ = 270° the distance is equal to ${\displaystyle p}$.
   At θ = 180°, aphelion, the distance is maximum (by definition, aphelion is – invariably – perihelion plus 180°)
   

   ${\displaystyle r_{\max }={\frac {p}{1-\varepsilon }}}$

   The semi-major axis a is the arithmetic mean between r_min and r_max:
   

   ${\displaystyle \,r_{\max }-a=a-r_{\min }}$

   ${\displaystyle a={\frac {p}{1-\varepsilon ^{2}}}}$

   The semi-minor axis b is the geometric mean between r_min and r_max:
   

   ${\displaystyle {\frac {r_{\max }}{b}}={\frac {b}{r_{\min }}}}$

   ${\displaystyle b={\frac {p}{\sqrt {1-\varepsilon ^{2}}}}}$

   The semi-latus rectum p is the harmonic mean between r_min and r_max:
   

   ${\displaystyle {\frac {1}{r_{\min }}}-{\frac {1}{p}}={\frac {1}{p}}-{\frac {1}{r_{\max }}}}$

   ${\displaystyle pa=r_{\max }r_{\min }=b^{2}\,}$

   The eccentricity ε is the coefficient of variation between r_min and r_max:
   

   ${\displaystyle \varepsilon ={\frac {r_{\max }-r_{\min }}{r_{\max }+r_{\min }}}.}$

   The area of the ellipse is
   

   ${\displaystyle A=\pi ab\,.}$

   The special case of a circle is ε = 0, resulting in r = p = r_min = r_max = a = b and A = πr².
   

   Second law

   A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.^[1]
   

   
   The same (blue) area is swept out in a fixed time period. The green arrow is velocity. The purple arrow directed towards the Sun is the acceleration. The other two purple arrows are acceleration components parallel and perpendicular to the velocity.
   The orbital radius and angular velocity of the planet in the elliptical orbit will vary. This is shown in the animation: the planet travels faster when closer to the sun, then slower when farther from the sun. Kepler's second law states that the blue sector has constant area.
   In a small time ${\displaystyle dt\,}$ the planet sweeps out a small triangle having base line ${\displaystyle r\,}$ and height ${\displaystyle r\,d\theta }$ and area ${\displaystyle dA={\tfrac {1}{2}}\cdot r\cdot rd\theta }$ and so the constant areal velocity is ${\displaystyle {\frac {dA}{dt}}={\tfrac {1}{2}}r^{2}{\frac {d\theta }{dt}}.}$
   The area enclosed by the elliptical orbit is ${\displaystyle \pi ab.\,}$ So the period ${\displaystyle P\,}$ satisfies
   

   ${\displaystyle P\cdot {\tfrac {1}{2}}r^{2}{\frac {d\theta }{dt}}=\pi ab}$

   and the mean motion of the planet around the Sun
   

   ${\displaystyle n=2\pi /P}$

   satisfies
   

   ${\displaystyle r^{2}\,d\theta =abn\,dt.}$

   Third law

   The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
   

   This captures the relationship between the distance of planets from the Sun, and their orbital periods.
   For a brief biography of Kepler and discussion of his third law, see: NASA: Stargaze.
   Kepler enunciated in 1619^[13] this third law in a laborious attempt to determine what he viewed as the "music of the spheres" according to precise laws, and express it in terms of musical notation.^[18] So it was known as the harmonic law.^[19]
   According to this law the expression P²a⁻³ has the same value for all the planets in the solar system. Here P is the time taken for a planet to complete an orbit round the sun, and a is the mean value between the maximum and minimum distances between the planet and sun.
   The corresponding formula in Newtonian mechanics is
   

   ${\displaystyle {\frac {P^{2}}{a^{3}}}={\frac {4\pi ^{2}}{G(M+m)}}\approx {\frac {4\pi ^{2}}{GM}}=\mathrm {constant} }$

   where M is the mass of the sun, m is the mass of the planet, and G is the gravitational constant.
   As the Sun is much heavier than any planet, Kepler's third law is approximately correct in Newtonian mechanics.
   

   Planetary acceleration

   Isaac Newton computed in his Philosophiæ Naturalis Principia Mathematica the acceleration of a planet moving according to Kepler's first and second law.
   
   1. The direction of the acceleration is towards the Sun.
   2. The magnitude of the acceleration is inversely proportional to the square of the planet's distance from the Sun (the inverse square law).
   This implies that the Sun may be the physical cause of the acceleration of planets. However, Newton states in his Principia that he considers forces from a mathematical point of view, not a physical, thereby taking an instrumentalist view.^[20] Moreover, he does not assign a cause to gravity.^[21]
   Newton defined the force acting on a planet to be the product of its mass and the acceleration (see Newton's laws of motion). So:
   
   1. Every planet is attracted towards the Sun.
   2. The force acting on a planet is in direct proportion to the mass of the planet and in inverse proportion to the square of its distance from the Sun.
   The Sun plays an unsymmetrical part, which is unjustified. So he assumed, in Newton's law of universal gravitation:
   
   1. All bodies in the solar system attract one another.
   2. The force between two bodies is in direct proportion to the product of their masses and in inverse proportion to the square of the distance between them.
   As the planets have small masses compared to that of the Sun, the orbits conform approximately to Kepler's laws. Newton's model improves upon Kepler's model, and fits actual observations more accurately (see two-body problem).
   Below comes the detailed calculation of the acceleration of a planet moving according to Kepler's first and second laws.
   

   Acceleration vector

   See also: Polar coordinate § Vector calculus, and Mechanics of planar particle motion
   From the heliocentric point of view consider the vector to the planet ${\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}$ where ${\displaystyle r}$ is the distance to the planet and ${\displaystyle {\hat {\mathbf {r} }}}$ is a unit vector pointing towards the planet.
   

   ${\displaystyle {\frac {d{\hat {\mathbf {r} }}}{dt}}={\dot {\hat {\mathbf {r} }}}={\dot {\theta }}{\hat {\boldsymbol {\theta }}},\qquad {\frac {d{\hat {\boldsymbol {\theta }}}}{dt}}={\dot {\hat {\boldsymbol {\theta }}}}=-{\dot {\theta }}{\hat {\mathbf {r} }}}$

   where ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ is the unit vector whose direction is 90 degrees counterclockwise of ${\displaystyle {\hat {\mathbf {r} }}}$, and ${\displaystyle \theta }$ is the polar angle, and where a dot on top of the variable signifies differentiation with respect to time.
   Differentiate the position vector twice to obtain the velocity vector and the acceleration vector:
   

   ${\displaystyle {\dot {\mathbf {r} }}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\hat {\mathbf {r} }}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},}$

   ${\displaystyle {\ddot {\mathbf {r} }}=({\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\hat {\mathbf {r} }}})+({\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\dot {\theta }}{\dot {\hat {\boldsymbol {\theta }}}})=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.}$

   So
   

   ${\displaystyle {\ddot {\mathbf {r} }}=a_{r}{\hat {\boldsymbol {r}}}+a_{\theta }{\hat {\boldsymbol {\theta }}}}$

   where the radial acceleration is
   

   ${\displaystyle a_{r}={\ddot {r}}-r{\dot {\theta }}^{2}}$

   and the transversal acceleration is
   

   ${\displaystyle a_{\theta }=r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}.}$

   The inverse square law

   Kepler's second law says that
   

   ${\displaystyle r^{2}{\dot {\theta }}=nab}$

   is constant.
   The transversal acceleration ${\displaystyle a_{\theta }}$ is zero:
   

   ${\displaystyle {\frac {d(r^{2}{\dot {\theta }})}{dt}}=r(2{\dot {r}}{\dot {\theta }}+r{\ddot {\theta }})=ra_{\theta }=0.}$

   So the acceleration of a planet obeying Kepler's second law is directed towards the sun.
   The radial acceleration ${\displaystyle a_{r}}$ is
   

   ${\displaystyle a_{r}={\ddot {r}}-r{\dot {\theta }}^{2}={\ddot {r}}-r\left({\frac {nab}{r^{2}}}\right)^{2}={\ddot {r}}-{\frac {n^{2}a^{2}b^{2}}{r^{3}}}.}$

   Kepler's first law states that the orbit is described by the equation:
   

   ${\displaystyle {\frac {p}{r}}=1+\varepsilon \cos \theta .}$

   Differentiating with respect to time
   

   ${\displaystyle -{\frac {p{\dot {r}}}{r^{2}}}=-\varepsilon \sin \theta \,{\dot {\theta }}}$

   or
   

   ${\displaystyle p{\dot {r}}=nab\,\varepsilon \sin \theta .}$

   Differentiating once more
   

   ${\displaystyle p{\ddot {r}}=nab\varepsilon \cos \theta \,{\dot {\theta }}=nab\varepsilon \cos \theta \,{\frac {nab}{r^{2}}}={\frac {n^{2}a^{2}b^{2}}{r^{2}}}\varepsilon \cos \theta .}$

   The radial acceleration ${\displaystyle a_{r}}$ satisfies
   

   ${\displaystyle pa_{r}={\frac {n^{2}a^{2}b^{2}}{r^{2}}}\varepsilon \cos \theta -p{\frac {n^{2}a^{2}b^{2}}{r^{3}}}={\frac {n^{2}a^{2}b^{2}}{r^{2}}}\left(\varepsilon \cos \theta -{\frac {p}{r}}\right).}$

   Substituting the equation of the ellipse gives
   

   ${\displaystyle pa_{r}={\frac {n^{2}a^{2}b^{2}}{r^{2}}}\left({\frac {p}{r}}-1-{\frac {p}{r}}\right)=-{\frac {n^{2}a^{2}}{r^{2}}}b^{2}.}$

   The relation ${\displaystyle b^{2}=pa}$ gives the simple final result
   

   ${\displaystyle a_{r}=-{\frac {n^{2}a^{3}}{r^{2}}}.}$

   This means that the acceleration vector ${\displaystyle \mathbf {\ddot {r}} }$ of any planet obeying Kepler's first and second law satisfies the inverse square law
   

   ${\displaystyle \mathbf {\ddot {r}} =-{\frac {\alpha }{r^{2}}}{\hat {\mathbf {r} }}}$

   where
   

   ${\displaystyle \alpha =n^{2}a^{3}\,}$

   is a constant, and ${\displaystyle {\hat {\mathbf {r} }}}$ is the unit vector pointing from the Sun towards the planet, and ${\displaystyle r\,}$ is the distance between the planet and the Sun.
   According to Kepler's third law, ${\displaystyle \alpha }$ has the same value for all the planets. So the inverse square law for planetary accelerations applies throughout the entire solar system.
   The inverse square law is a differential equation. The solutions to this differential equation include the Keplerian motions, as shown, but they also include motions where the orbit is a hyperbola or parabola or a straight line. See Kepler orbit.
   

   Newton's law of gravitation

   By Newton's second law, the gravitational force that acts on the planet is:
   

   ${\displaystyle \mathbf {F} =m_{\text{planet}}\mathbf {\ddot {r}} =-m_{\text{planet}}\alpha r^{-2}{\hat {\mathbf {r} }}}$

   where ${\displaystyle m_{\text{planet}}}$ is the mass of the planet and ${\displaystyle \alpha }$ has the same value for all planets in the solar system. According to Newton's third Law, the Sun is attracted to the planet by a force of the same magnitude. Since the force is proportional to the mass of the planet, under the symmetric consideration, it should also be proportional to the mass of the Sun, ${\displaystyle m_{\text{Sun}}}$. So
   

   ${\displaystyle \alpha =Gm_{\text{Sun}}}$

   where ${\displaystyle G}$ is the gravitational constant.
   The acceleration of solar system body number i is, according to Newton's laws:
   

   ${\displaystyle \mathbf {{\ddot {r}}_{i}} =G\sum _{j\neq i}m_{j}r_{ij}^{-2}{\hat {\mathbf {r} }}_{ij}}$

   where ${\displaystyle m_{j}}$ is the mass of body j, ${\displaystyle r_{ij}}$ is the distance between body i and body j, ${\displaystyle {\hat {\mathbf {r} }}_{ij}}$ is the unit vector from body i towards body j, and the vector summation is over all bodies in the world, besides i itself.
   In the special case where there are only two bodies in the world, Earth and Sun, the acceleration becomes
   

   ${\displaystyle \mathbf {\ddot {r}} _{\text{Earth}}=Gm_{\text{Sun}}r_{{\text{Earth}},{\text{Sun}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Earth}},{\text{Sun}}}}$

   which is the acceleration of the Kepler motion. So this Earth moves around the Sun according to Kepler's laws.
   If the two bodies in the world are Moon and Earth the acceleration of the Moon becomes
   

   ${\displaystyle \mathbf {\ddot {r}} _{\text{Moon}}=Gm_{\text{Earth}}r_{{\text{Moon}},{\text{Earth}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Moon}},{\text{Earth}}}}$

   So in this approximation the Moon moves around the Earth according to Kepler's laws.
   In the three-body case the accelerations are
   

   ${\displaystyle \mathbf {\ddot {r}} _{\text{Sun}}=Gm_{\text{Earth}}r_{{\text{Sun}},{\text{Earth}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Sun}},{\text{Earth}}}+Gm_{\text{Moon}}r_{{\text{Sun}},{\text{Moon}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Sun}},{\text{Moon}}}}$

   ${\displaystyle \mathbf {\ddot {r}} _{\text{Earth}}=Gm_{\text{Sun}}r_{{\text{Earth}},{\text{Sun}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Earth}},{\text{Sun}}}+Gm_{\text{Moon}}r_{{\text{Earth}},{\text{Moon}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Earth}},{\text{Moon}}}}$

   ${\displaystyle \mathbf {\ddot {r}} _{\text{Moon}}=Gm_{\text{Sun}}r_{{\text{Moon}},{\text{Sun}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Moon}},{\text{Sun}}}+Gm_{\text{Earth}}r_{{\text{Moon}},{\text{Earth}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Moon}},{\text{Earth}}}}$

   These accelerations are not those of Kepler orbits, and the three-body problem is complicated. But Keplerian approximation is the basis for perturbation calculations. See Lunar theory.
   

   Position as a function of time

   Kepler used his two first laws to compute the position of a planet as a function of time. His method involves the solution of a transcendental equation called Kepler's equation.
   The procedure for calculating the heliocentric polar coordinates (r,θ) of a planet as a function of the time t since perihelion, is the following four steps:
   

   1. Compute the mean anomaly M = nt where n is the mean motion.

   ${\displaystyle n\cdot P=2\pi }$ radians where P is the period.

   2. Compute the eccentric anomaly E by solving Kepler's equation:

   ${\displaystyle \ M=E-\varepsilon \sin E}$

   3. Compute the true anomaly θ by the equation:

   ${\displaystyle (1-\varepsilon )\tan ^{2}{\frac {\theta }{2}}=(1+\varepsilon )\tan ^{2}{\frac {E}{2}}}$

   4. Compute the heliocentric distance

   ${\displaystyle r=a(1-\varepsilon \cos E).}$

   The important special case of circular orbit, ε = 0, gives θ = E = M. Because the uniform circular motion was considered to be normal, a deviation from this motion was considered an anomaly.
   The proof of this procedure is shown below.
   

   Mean anomaly, M

   
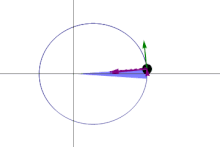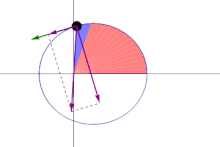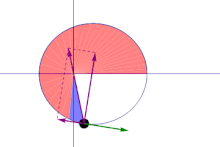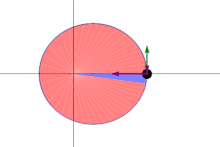
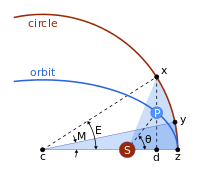
   FIgure 5: Geometric construction for Kepler's calculation of θ. The Sun (located at the focus) is labeled S and the planet P. The auxiliary circle is an aid to calculation. Line xd is perpendicular to the base and through the planet P. The shaded sectors are arranged to have equal areas by positioning of point y.
   The Keplerian problem assumes an elliptical orbit and the four points:
   

   s the Sun (at one focus of ellipse);

   z the perihelion

   c the center of the ellipse

   p the planet

   and
   

   ${\displaystyle \ a=|cz|,}$ distance between center and perihelion, the semimajor axis,

   ${\displaystyle \ \varepsilon ={|cs| \over a},}$ the eccentricity,

   ${\displaystyle \ b=a{\sqrt {1-\varepsilon ^{2}}},}$ the semiminor axis,

   ${\displaystyle \ r=|sp|,}$ the distance between Sun and planet.

   ${\displaystyle \theta =\angle zsp,}$ the direction to the planet as seen from the Sun, the true anomaly.

   The problem is to compute the polar coordinates (r,θ) of the planet from the time since perihelion, t.
   It is solved in steps. Kepler considered the circle with the major axis as a diameter, and
   

   ${\displaystyle \ x,}$ the projection of the planet to the auxiliary circle

   ${\displaystyle \ y,}$ the point on the circle such that the sector areas |zcy| and |zsx| are equal,

   ${\displaystyle M=\angle zcy,}$ the mean anomaly.

   The sector areas are related by ${\displaystyle |zsp|={\frac {b}{a}}\cdot |zsx|.}$
   The circular sector area ${\displaystyle \ |zcy|={\frac {a^{2}M}{2}}.}$
   The area swept since perihelion,
   

   ${\displaystyle |zsp|={\frac {b}{a}}\cdot |zsx|={\frac {b}{a}}\cdot |zcy|={\frac {b}{a}}\cdot {\frac {a^{2}M}{2}}={\frac {abM}{2}},}$

   is by Kepler's second law proportional to time since perihelion. So the mean anomaly, M, is proportional to time since perihelion, t.
   

   ${\displaystyle M=nt,\,}$

   where n is the mean motion.
   

   Eccentric anomaly, E

   When the mean anomaly M is computed, the goal is to compute the true anomaly θ. The function θ = f(M) is, however, not elementary.^[22] Kepler's solution is to use
   

   ${\displaystyle E=\angle zcx}$, x as seen from the centre, the eccentric anomaly

   as an intermediate variable, and first compute E as a function of M by solving Kepler's equation below, and then compute the true anomaly θ from the eccentric anomaly E. Here are the details.
   

   ${\displaystyle \ |zcy|=|zsx|=|zcx|-|scx|}$

   ${\displaystyle {\frac {a^{2}M}{2}}={\frac {a^{2}E}{2}}-{\frac {a\varepsilon \cdot a\sin E}{2}}}$

   Division by a²/2 gives Kepler's equation
   

   ${\displaystyle M=E-\varepsilon \cdot \sin E.}$

   This equation gives M as a function of E. Determining E for a given M is the inverse problem. Iterative numerical algorithms are commonly used.
   Having computed the eccentric anomaly E, the next step is to calculate the true anomaly θ.
   

   True anomaly, θ

   Note from the figure that
   

   ${\displaystyle {\overrightarrow {cd}}={\overrightarrow {cs}}+{\overrightarrow {sd}}}$

   so that
   

   ${\displaystyle a\cdot \cos E=a\cdot \varepsilon +r\cdot \cos \theta .}$

   Dividing by ${\displaystyle a}$ and inserting from Kepler's first law
   

   ${\displaystyle \ {\frac {r}{a}}={\frac {1-\varepsilon ^{2}}{1+\varepsilon \cdot \cos \theta }}}$

   to get
   

   ${\displaystyle \cos E=\varepsilon +{\frac {1-\varepsilon ^{2}}{1+\varepsilon \cdot \cos \theta }}\cdot \cos \theta }$ ${\displaystyle ={\frac {\varepsilon \cdot (1+\varepsilon \cdot \cos \theta )+(1-\varepsilon ^{2})\cdot \cos \theta }{1+\varepsilon \cdot \cos \theta }}}$ ${\displaystyle ={\frac {\varepsilon +\cos \theta }{1+\varepsilon \cdot \cos \theta }}.}$

   The result is a usable relationship between the eccentric anomaly E and the true anomaly θ.
   A computationally more convenient form follows by substituting into the trigonometric identity:
   

   ${\displaystyle \tan ^{2}{\frac {x}{2}}={\frac {1-\cos x}{1+\cos x}}.}$

   Get
   

   ${\displaystyle {\begin{aligned}&\tan ^{2}{\frac {E}{2}}={\frac {1-\cos E}{1+\cos E}}={\frac {1-{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cdot \cos \theta }}}{1+{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cdot \cos \theta }}}}\\[8pt]={}&{\frac {(1+\varepsilon \cdot \cos \theta )-(\varepsilon +\cos \theta )}{(1+\varepsilon \cdot \cos \theta )+(\varepsilon +\cos \theta )}}={\frac {1-\varepsilon }{1+\varepsilon }}\cdot {\frac {1-\cos \theta }{1+\cos \theta }}={\frac {1-\varepsilon }{1+\varepsilon }}\cdot \tan ^{2}{\frac {\theta }{2}}.\end{aligned}}}$

   Multiplying by 1 + ε gives the result
   

   ${\displaystyle (1-\varepsilon )\cdot \tan ^{2}{\frac {\theta }{2}}=(1+\varepsilon )\cdot \tan ^{2}{\frac {E}{2}}}$

   This is the third step in the connection between time and position in the orbit.
   

   Distance, r

   The fourth step is to compute the heliocentric distance r from the true anomaly θ by Kepler's first law:
   

   ${\displaystyle \ r\cdot (1+\varepsilon \cdot \cos \theta )=a\cdot (1-\varepsilon ^{2})}$

   Using the relation above between θ and E the final equation for the distance r is:
   

   ${\displaystyle \ r=a\cdot (1-\varepsilon \cdot \cos E).}$

   See also

   • Circular motion
   • Free-fall time
   • Gravity
   • Kepler orbit
   • Kepler problem
   • Kepler's equation
   • Laplace–Runge–Lenz vector
   • Specific relative angular momentum, relatively easy derivation of Kepler's laws starting with conservation of angular momentum

   Notes

2. 
   
Godefroy Wendelin wrote a letter to Giovanni Battista Riccioli about the relationship between the distances of the Jovian moons from Jupiter and the periods of their orbits, showing that the periods and distances conformed to Kepler's third law. See: Joanne Baptista Riccioli, Almagestum novum … (Bologna (Bononia), (Italy): Victor Benati, 1651), volume 1, page 492 Scholia III. In the margin beside the relevant paragraph is printed: Vendelini ingeniosa speculatio circa motus & intervalla satellitum Jovis. (Wendelin's clever speculation about the movement and distances of Jupiter's satellites.)
In 1621, Johannes Kepler had noted that Jupiter's moons obey (approximately) his third law in his Epitome Astronomiae Copernicanae [Epitome of Copernican Astronomy] (Linz (“Lentiis ad Danubium“), (Austria): Johann Planck, 1622)